La didattica della scienza è spesso al centro di vivaci dibattiti, e sempre più sorgono proposte di scienze e/o attività tecnologiche per bambini. Tuttavia, si tralascia spesso il come sia opportuno svolgere la didattica, e ci si concentra troppo sul cosa si debba fare durante i laboratori e le lezioni di scienze (o di matematica, la situazione è analoga). Quali esperimenti fantasmagorici possiamo far svolgere ai bambini? Quali software rivoluzionari possiamo mettere loro davanti? Ma il come questi laboratori vadano condotti, a cosa sia opportuno fare attenzione, questa sono spesso faccende più trascurate.
Permetteteci una breve riflessione su quale come noi riteniamo importante quando si tratta di scienze o matematica con i più piccoli.
Il come della didattica della scienza
Sarebbe bene che chi desidera proporre attività a sfondo scientifico (a ogni livello, ma in particolare per bambini) si esercitasse nell’arte della narrazione, e affinasse le sue capacità di scrittura.
Questo perchè un incontro di scienze è prima di tutto una storia! E ciò vale da molti punti di vista. Per primo, l’incontro in sè, comunque sia strutturato, deve avere una struttura ben chiara nella mente dell’organizzatore. Capita sempre che il piano iniziale venga sconvolto dall’interazione con i bimbi, ma l’educatore deve arrivare avendo chiara in testa una scaletta dell’attività. La giornata ha un incipt, un explicit, ma soprattutto un punto di climax! E, come in ogni storia, l’incipit deve catturare, l’explicit sviluppare il desiderio della prossima storia, e il climax deve essere valorizzato!
Lo stesso si applica a “dimensioni” differenti: non solo l’intera giornata in sè ha la struttura di una storia, ma anche lo stesso svolgimento di un esperimento. Proporre un’attività scientifica come una serie di passi da seguire ha lo stesso effetto che proporre il riassunto di un racconto: il contenuto c’è tutto, ma il suo scopo è solo quello di fornire delle informazioni, non di coinvolgere e invitare alla lettura. Allo stesso modo, se si propone ai bambini solo di seguire delle istruzioni, non si invita alla scoperta, all’esplorazione, alla creazione di qualcosa, ma solo a cucinare una ricetta che qualcun altro ha progettato. E’ chiaro che noi, dal ruolo di educatori, conosciamo la ricetta; ma, nel proporla ai nostri provetti cuochi, il nostro ruolo richiede proprio che confezioniamo tale serie di passi in una storia con una struttura.
Continua la lettura di Una riflessione sullo stato della didattica della scienza
Si può provare a sottoporre al bimbo la questione nello stesso modo in cui sarebbe opportuno presentargli la moltiplicazione per la prima volta: attraverso un conteggio esplicito. Basta procurarsi una decina di furgoncini giocattolo e una cinquantina di caramelle per un’approccio diverso alle moltiplicazioni per dieci. Tale metodo è particolarmente efficace per bimbi piccoli, basta che sappiano contare almeno fino a 30!
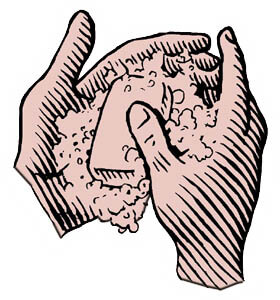
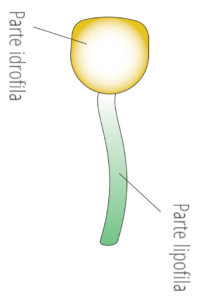Per capire bene come funziona il sapone, proviamo ora a immaginare cosa accade quando ci laviamo le mani. Quando le insaponiamo, ogni molecola di sapone si attacca con la coda a una molecola di sporco (che tipicamente è di natura grassa). La testa delle molecole di sapone rimane tuttavia libera, perché abbiamo visto che è così che al sapone piace fare. In effetti, le molecole di sapone sono davvero una folla numerosissima, perché ogni molecola di sporco non viene agganciata da una sola molecola di sapone, ma normalmente ci sono molte molecole di sapone per una sola di sporco!
Dato che la divisione è l’operazione inversa della moltiplicazione, e lo stesso vale per la sottrazione rispetto alla somma, possiamo limitarci a parlare del per e del più.
, immagino di avere 3 arance da una parte, 2 arance dall’altra, di metterle tutte vicine e poi contare fino a 5.
. Ci sono due modi di svolgerla: fare prima il per e poi il più, oppure viceversa. Facciamo le prove e vediamo se deve lavorare di più se prima fa la moltiplicazione o se prima fa la somma.