Un semplice indovinello sul coronavirus (covid) per bambini, ma scritto con un alfabeto cifrato. Clicca sull’immagine per scaricare il pdf di 3 pagine.
La didattica della scienza è spesso al centro di vivaci dibattiti, e sempre più sorgono proposte di scienze e/o attività tecnologiche per bambini. Tuttavia, si tralascia spesso il come sia opportuno svolgere la didattica, e ci si concentra troppo sul cosa si debba fare durante i laboratori e le lezioni di scienze (o di matematica, la situazione è analoga). Quali esperimenti fantasmagorici possiamo far svolgere ai bambini? Quali software rivoluzionari possiamo mettere loro davanti? Ma il come questi laboratori vadano condotti, a cosa sia opportuno fare attenzione, questa sono spesso faccende più trascurate.
Permetteteci una breve riflessione su quale come noi riteniamo importante quando si tratta di scienze o matematica con i più piccoli.
Sarebbe bene che chi desidera proporre attività a sfondo scientifico (a ogni livello, ma in particolare per bambini) si esercitasse nell’arte della narrazione, e affinasse le sue capacità di scrittura.
Questo perchè un incontro di scienze è prima di tutto una storia! E ciò vale da molti punti di vista. Per primo, l’incontro in sè, comunque sia strutturato, deve avere una struttura ben chiara nella mente dell’organizzatore. Capita sempre che il piano iniziale venga sconvolto dall’interazione con i bimbi, ma l’educatore deve arrivare avendo chiara in testa una scaletta dell’attività. La giornata ha un incipt, un explicit, ma soprattutto un punto di climax! E, come in ogni storia, l’incipit deve catturare, l’explicit sviluppare il desiderio della prossima storia, e il climax deve essere valorizzato!
Lo stesso si applica a “dimensioni” differenti: non solo l’intera giornata in sè ha la struttura di una storia, ma anche lo stesso svolgimento di un esperimento. Proporre un’attività scientifica come una serie di passi da seguire ha lo stesso effetto che proporre il riassunto di un racconto: il contenuto c’è tutto, ma il suo scopo è solo quello di fornire delle informazioni, non di coinvolgere e invitare alla lettura. Allo stesso modo, se si propone ai bambini solo di seguire delle istruzioni, non si invita alla scoperta, all’esplorazione, alla creazione di qualcosa, ma solo a cucinare una ricetta che qualcun altro ha progettato. E’ chiaro che noi, dal ruolo di educatori, conosciamo la ricetta; ma, nel proporla ai nostri provetti cuochi, il nostro ruolo richiede proprio che confezioniamo tale serie di passi in una storia con una struttura.
Continua la lettura di Una riflessione sullo stato della didattica della scienza
Una macchina che si muove grazie a un palloncino, sfrecciando su ruote dolciastre? Si può costruire, e con poco!
Bastano pochi semplici materiali, economici e reperibili nei negozi, per realizzare una macchina avente come ruote della caramelle e spinta da un palloncino.
Un’attività semplice, che consente di sperimentare il funzionamento del terzo principio della dinamica, anche conosciuto come principio di azione-reazione.
Cominciamo col predisporre il corpo della macchina, costituito dal cartoncino. Si può sperimentare alla ricerca della forma più aerodinamica, ma la dimensione di una cartolina è ottima per una macchina leggera, veloce, e comunque resistente.
Poi, il primo passaggio della costruzione vera e proprio consiste nel tagliare la parte pieghevole da due cannucce, se presente. Le cannucce faranno da sostegno alle ruote. Una volta tagliate le estremità, usiamo lo scotch per attaccare le cannucce al cartoncino. Cerchiamo di posizionarle ben perpendicolari ai bordi del cartoncino e di farle uscire dal bordo del cartoncino in egual misura. L’attenzione alla simmetria serve per evitare che la macchina, alla fine della costruzione, vada storta.
Continua la lettura di Costruire una macchina a caramelle e palloncini
Schiacciare forte dello zucchero per ottenere… un po’ di luce? Unire e separare scotch da pacchi per scoprire un piccolo bagliore bluastro? Sembra assurdo, e invece è… triboluminescenza!
Ci sono due piccoli esperimenti riguardanti la triboluminescenza che si possono facilmente realizzare a casa. Si tratta di un fenomeno alquanto insolito. L’unico reale requisito è una stanza buia, davvero buia, possibilmente senza finestre, come una dispensa.
Il primo esperimento richiede una zolletta (o manciata) di zucchero e un paio di pinze. Anche alcune caramelle di zucchero vanno bene. Ponete la zolletta nelle pinze e immergetevi nell’oscurità. Portate le pinze a livello degli occhi per poter vedere ciò che accade, e schiacciate fortissimo. Noterete un piccolo bagliore bluastro, che nasce e muore nel momento in cui lo zucchero viene compresso.
Continua la lettura di La triboluminescenza: dallo zucchero alla luce!
Il Piacere di Scoprire e organizza cicli di laboratori scientifici per bambini e ragazzi un pomeriggio a settimana. Desideriamo esplorare la natura per il gusto di scoprire cose nuove e divertirci. Ci vediamo un pomeriggio a settimana nei pressi di Spianata Castelletto (età indicativa 6-10). Per scoprire di più sullo spirito e le intenzioni degli incontri, vai a Una nuova casa sull’albero per piccoli scienziati. Per avere informazioni sugli incontri, iscrivere tuo figlio e comunicare con noi, contattaci!
Riassunto per i pigrissimi: Dopo il grande successo degli anni passati, Il Piacere di Scoprire è pronto a ripartire! Organizziamo cicli di laboratori scientifici per bambini un pomeriggio a settimana. Desideriamo tornare a esplorare la natura per il gusto di scoprire cose nuove e divertirci. Ci vediamo il 29 Settembre alle 16 vicino a Castelletto con un incontro conoscitivo per adulti e un laboratorio gratuito per bambini (età indicativa 6-10). Qui l’evento Facebook. Se proprio non puoi leggere il resto, salta alla sezione “Lista delle cose da fare”.
Viviamo in un mondo di risultati e di aspettative. Un mondo in cui le cose si fanno per un fine, e la metrica di giudizio è il successo. Un mondo in cui si fanno i compiti per essere pronti alla verifica in classe, in cui si studia per passare gli esami, in cui si fanno esperienze extra per arricchire il curriculum in vista del lavoro… Sempre più spesso tendiamo a fare qualcosa con la chiara prospettiva del a cosa questo serva nella nostra vita. Ma non è forse più importante il cammino della meta? Il viaggio, della destinazione?
Per questo noi vorremmo proporre una prospettiva diversa. Vorremmo davvero tornare a fare le cose perché ci fa piacere farle, e perché stimolano il nostro interesse e sviluppo. Desideriamo creare uno spazio di esplorazione: un luogo in cui il motore sia il piacere di scoprire cose nuove.
Vorremmo promuovere una conoscenza disinteressata, perché è la più potente di tutte. Le cose che impariamo per noi stessi le potremo mettere a frutto in qualunque circostanza della nostra vita: una verifica, un esame, un lavoro. Ma soprattutto, ci renderà la vita più luminosa! C’è così tanto da scoprire che vale la pena esplorare! Siamo spesso trattenuti dalla paura che il nostro bambino non trovi il suo posto nel mondo. Tuttavia, non dobbiamo lasciare che questo gli impedisca di trovare, appunto, il suo posto, e non un posto qualunque. Se vuole mollare l’università e seguire un corso di calligrafia incoraggiatelo: è quello che ha fatto Steve Jobs, e nessuno lo classifica come un fallito. Come ci insegna Maria Montessori, ogni attività che non sia chiaramente dannosa per il bambino è funzionale al suo sviluppo.
In questo consiste quindi il nostro progetto: creare uno spazio di crescita ed esplorazione disinteressata per bambini e ragazzi a Genova, che spalanchi davanti a loro le porte del futuro e lo renda più felice.
Continua la lettura di Una nuova casa sull’albero per piccoli scienziati
Scopriamo come costruire una macchina fotografica fatta in casa, per scattare foto con un oggetto creato da noi. Materiali di recupero ci permetteranno di immortalare i momenti più belli!
Bastano dei semplici materiali e un po’ di ingegno per costruire una macchina fotografica!
Non sarà una macchina fotografica digitale di ultima generazione, ma – ancora meglio! – un’occasione per riscoprire le macchine a pellicola, quelle di primissima generazione: le macchine fotografiche a foro stenopeico. I bimbi non sanno che fino a pochi anni fa le fotografie non erano registrate su uno schermo luminoso – e facciamoglielo fare, questo salto nel passato! Costruire una macchina fotografica sarà l’occasione per scoprirne il funzionamento!
Il primo passo per costruire una macchina fotografica è prendere la scatola e aprirla ai lati. In altre parole, quello che ci serve della scatola è il suo cartoncino e le sue pieghe, ma non la sua struttura.
Dobbiamo poi prendere le misure affinché la scatola abbia la dimensione necessaria per diventare una macchina fotografica: useremo il rullino per prendere la misura.
Prendiamo allora il rullino e posiamolo sul lato lungo della scatola, facendone coincidere la base con lo spigolo. Con un pennarello segniamo l’altezza del rullino e tiriamo una riga fino all’altro lato della scatola. È importante fare attenzione a prendere la misura sotto il piccolo cilindro sporgente in cima: consideriamo solo il corpo principale del rullino. Ripetiamo poi il procedimento uguale sull’altra faccia della scatola.
Perché non si può dividere per zero? Cosa ha di così speciale questo numero per rendere la divisione impossibile?
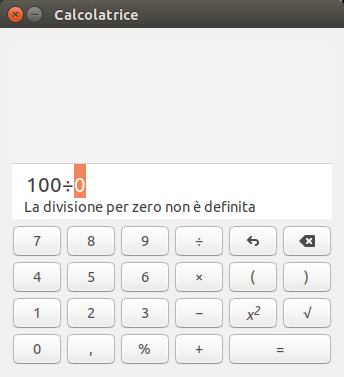Avete mai provato a dividere un numero per zero con la calcolatrice? Se provate, scoprirete che anche la calcolatrice si rifiuta di farlo! E, in effetti, a scuola ci hanno sempre detto che non si può fare: non si può dividere per zero.
Ma in matematica tutte le cose hanno una ragione, e la divisione per zero non fa eccezione. Cerchiamo di scoprire perché non si possa dividere per zero, con una spiegazione che anche i bimbi possono capire!
Tutte le volte che in matematica si dà una risposta a un problema, è importante che tale risposta sia sensata. Non giusta, ma sensata! Dare una risposta sensata, in effetti, è fin più importante della sua esattezza… Nel caso della divisione per zero, il problema è che non è possibile trovare una risposta sensata. Per scoprire perché, facciamo un piccolo viaggio tra i numeri!
Per cominciare, proviamo a vedere cosa succede a dividere il numero dieci per dei numeri che diventano via via più piccoli.
| Dividendo | Divisore | Risultato | |
| 10 |  |
5 | 2 |
| 10 | |
3 | 3.33 |
| 10 | |
2 | 5 |
| 10 | |
1 | 10 |
| 10 | |
0.5 | 20 |
| 10 | |
0.25 | 40 |
| 10 | |
0.10 | 100 |
| 10 | |
0.05 | 200 |
| 10 | |
0.01 | 1000 |
| 10 | |
0.001 | 10000 |
Fermiamoci a osservare questi numeri: più il numero per cui dividiamo diventa piccolo, più il risultato diventa grande! E allora, cosa succederebbe se dividessimo proprio per zero? Sembra, fin qui che verrebbe infinito! Infinito non è un numero come tutti gli altri, ma è pur sempre una risposta… ed è sensata! Ma perché allora non va bene?
Continua la lettura di Dividere per zero: perché non si può fare?
Come stimolare la creatività dei bambini? Con pochi semplici materiali e un pizzico di fantasia, scopriamo come costruire un acchiappasogni. Lo potremo appendere in camera per scacciare i brutti sogni!
Basta un po’ di colla e qualche goccia di coloranti alimentari per realizzare un acchiappasogni con una tecnica pittorica insolita. Scopriamo come realizzare in modo semplice un oggetto che darà la possibilità ai bambini di esprimere le proprie abilità artistiche!
Prepariamo un tavolo dove i bambini potranno poggiarsi per creare l’acchiappasogni. Useremo dei coloranti, seppur alimentari: quindi prendiamo provvedimenti per non sporcarci. Per cominciare, prendiamo il piatto di plastica: sarà la base dell’acchiappasogni.
Prendiamo poi la colla e, con il pennello, spargiamola delicatamente nell’interno del piatto. Il piatto deve essere ruvido, in modo che la colla, grazie ai tanti piccoli solchi, si disponga uniformemente e faccia presa. Alla fine taglieremo via il contorno del piatto, quindi ricordiamoci di non disegnare nulla in quella parte!
Stiamo attenti a quanta colla mettiamo. Infatti, non dobbiamo metterne uno strato troppo spesso, altrimenti il colorante verrà poi assorbito e rimarrà praticamente solo la colla. In questo caso, il disegno rimarrà molto sbiadito. Ma non dobbiamo neanche mettere uno strato troppo sottile perché altrimenti la colla asciugherà in fretta e ci sarà poco tempo per disegnare.
Continua la lettura di Costruire un acchiappasogni con colla e colori